In this post, we will talk about Problem Solving agents in Artificial Intelligence, which are sort of goal-based agents. Because the straight mapping from states to actions of a basic reflex agent is too vast to retain for a complex environment, we utilize goal-based agents that may consider future actions and the desirability of outcomes.
Problem Solving Agents
Problem Solving Agents decide what to do by finding a sequence of actions that leads to a desirable state or solution.
An agent may need to plan when the best course of action is not immediately visible. They may need to think through a series of moves that will lead them to their goal state. Such an agent is known as a problem solving agent, and the computation it does is known as a search.
The problem solving agent follows this four phase problem solving process:
- Goal Formulation: This is the first and most basic phase in problem solving. It arranges specific steps to establish a target/goal that demands some activity to reach it. AI agents are now used to formulate goals.
- Problem Formulation: It is one of the fundamental steps in problem-solving that determines what action should be taken to reach the goal.
- Search: After the Goal and Problem Formulation, the agent simulates sequences of actions and has to look for a sequence of actions that reaches the goal. This process is called search, and the sequence is called a solution. The agent might have to simulate multiple sequences that do not reach the goal, but eventually, it will find a solution, or it will find that no solution is possible. A search algorithm takes a problem as input and outputs a sequence of actions.
- Execution: After the search phase, the agent can now execute the actions that are recommended by the search algorithm, one at a time. This final stage is known as the execution phase.
Problems and Solution
Before we move into the problem formulation phase, we must first define a problem in terms of problem solving agents.
A formal definition of a problem consists of five components:
- Initial State
- Actions
- Transition Model
- Goal Test
- Path Cost
Initial State
It is the agent’s starting state or initial step towards its goal. For example, if a taxi agent needs to travel to a location(B), but the taxi is already at location(A), the problem’s initial state would be the location (A).
Actions
It is a description of the possible actions that the agent can take. Given a state s, Actions(s) returns the actions that can be executed in s. Each of these actions is said to be appropriate in s.
Transition Model
It describes what each action does. It is specified by a function Result(s, a) that returns the state that results from doing action an in state s.
The initial state, actions, and transition model together define the state space of a problem, a set of all states reachable from the initial state by any sequence of actions. The state space forms a graph in which the nodes are states, and the links between the nodes are actions.
Goal Test
It determines if the given state is a goal state. Sometimes there is an explicit list of potential goal states, and the test merely verifies whether the provided state is one of them. The goal is sometimes expressed via an abstract attribute rather than an explicitly enumerated set of conditions.
Path Cost
It assigns a numerical cost to each path that leads to the goal. The problem solving agents choose a cost function that matches its performance measure. Remember that the optimal solution has the lowest path cost of all the solutions.
Example Problems
The problem solving approach has been used in a wide range of work contexts. There are two kinds of problem approaches
- Standardized/ Toy Problem: Its purpose is to demonstrate or practice various problem solving techniques. It can be described concisely and precisely, making it appropriate as a benchmark for academics to compare the performance of algorithms.
- Real-world Problems: It is real-world problems that need solutions. It does not rely on descriptions, unlike a toy problem, yet we can have a basic description of the issue.
Some Standardized/Toy Problems
Vacuum World Problem
Let us take a vacuum cleaner agent and it can move left or right and its jump is to suck up the dirt from the floor.
A grid world problem is a two-dimensional rectangular array of square cells through which agents can move. Typically, the agent can go to any nearby cell that is clear of obstacles, either horizontally or vertically, and in rare cases diagonally. A wall or other impassible obstruction in a cell prohibits an agent from moving inside that cell.
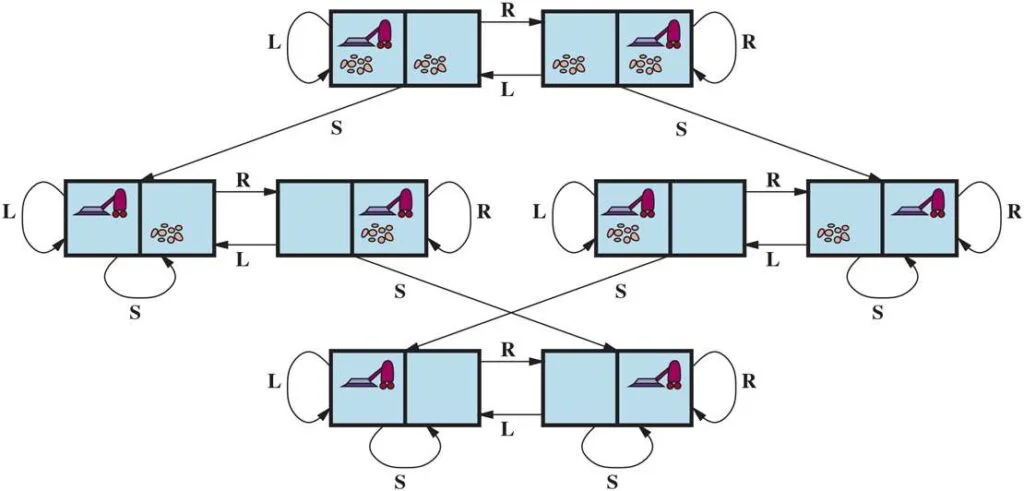
The vacuum world’s problem can be stated as follows:
States: A world state specifies which objects are housed in which cells. The objects in the vacuum world are the agent and any dirt. The agent can be in either of the two cells in the simple two-cell version, and each call can include dirt or not, therefore there are 2×2×2 = 8 states. A vacuum environment with n cells has n×2n states in general.
Initial State: Any state can be specified as the starting point.
Actions: We defined three actions in the two-cell world: sucking, moving left, and moving right. More movement activities are required in a two-dimensional multi-cell world.
Transition Model: Suck cleans the agent’s cell of any filth; Forward moves the agent one cell forward in the direction it is facing unless it meets a wall, in which case the action has no effect. Backward moves the agent in the opposite direction, whilst TurnRight and TurnLeft rotate it by 90°.
Goal States: The states in which every cell is clean.
Action Cost: Each action costs 1.
8 Puzzle Problem
In a sliding-tile puzzle, a number of tiles (sometimes called blocks or pieces) are arranged in a grid with one or more blank spaces so that some of the tiles can slide into the blank space. One variant is the Rush Hour puzzle, in which cars and trucks slide around a 6 x 6 grid in an attempt to free a car from the traffic jam. Perhaps the best-known variant is the 8- puzzle (see Figure below ), which consists of a 3 x 3 grid with eight numbered tiles and one blank space, and the 15-puzzle on a 4 x 4 grid. The object is to reach a specified goal state, such as the one shown on the right of the figure. The standard formulation of the 8 puzzles is as follows:
STATES: A state description specifies the location of each of the tiles.
INITIAL STATE: Any state can be designated as the initial state. (Note that a parity property partitions the state space—any given goal can be reached from exactly half of the possible initial states.)
ACTIONS: While in the physical world it is a tile that slides, the simplest way of describing action is to think of the blank space moving Left, Right, Up, or Down. If the blank is at an edge or corner then not all actions will be applicable.
TRANSITION MODEL: Maps a state and action to a resulting state; for example, if we apply Left to the start state in the Figure below, the resulting state has the 5 and the blank switched.
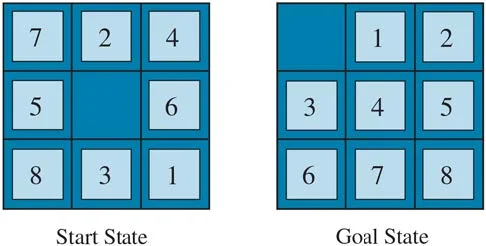
GOAL STATE: It identifies whether we have reached the correct goal state. Although any state could be the goal, we typically specify a state with the numbers in order, as in the Figure above.
ACTION COST: Each action costs 1.

