Breadth First Search (BFS) is a traversing algorithm that requires you to begin traversing from a specific node (the source or starting node) and traverse the graph layer by layer, thus exploring the neighbor nodes (nodes that are directly connected to source node). Then you must proceed to the next-level neighbor nodes. Extra memory, usually a queue, is needed to track the child nodes encountered but not yet explored.
As the name BFS suggests, you are required to traverse the graph breadthwise as follows:
- First, move horizontally and visit all the nodes of the current layer
- Move to the next layer
Consider the following diagram.
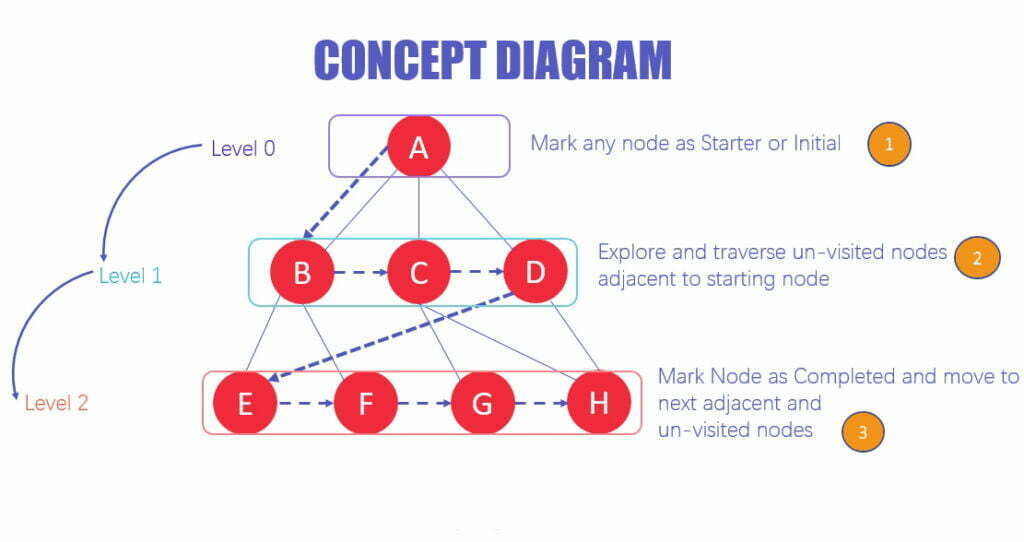
The distance between nodes in layer 1 is less than between nodes in layer 2. As a result, in BFS, you must first traverse all nodes in layer 1 before proceeding to nodes in layer 2.
A standard BFS implementation puts each vertex of the graph into one of two categories:
- Visited
- Not VIsited
BFS Algorithm
The Breadth First Search algorithm works as follows:
- Start by putting any of the graph’s vertices at the back of a queue.
- Take the front item of the queue and add it to the visited list.
- Create a list of that vertex’s adjacent nodes. Add the ones which aren’t in the visited list to the back of the queue.
- Keep repeating steps 2 and 3 until the queue is empty.
Breadth First Search in Python
Graph={}
n = int(input("Number of Vertices: "))
for i in range(n):
k = input("Enter the Node: ")
v = []
w = int(input("How many Adjacent Vertices you have for this Node? "))
for m in range(w):
v+=input("Enter the Vertices: ")
Graph.update({k:v})
visited=[]
queue=[]
def bfs(visited, Graph, current_node):
global queue
visited+=current_node
queue+=current_node
while queue:
a=queue.pop(0)
print(f"BFS:{a}", end = " ")
for child in Graph[a]:
if child not in visited:
visited+=child
queue+=child
res = list(Graph.keys())[0]
bfs(visited, Graph, res)Input & Output
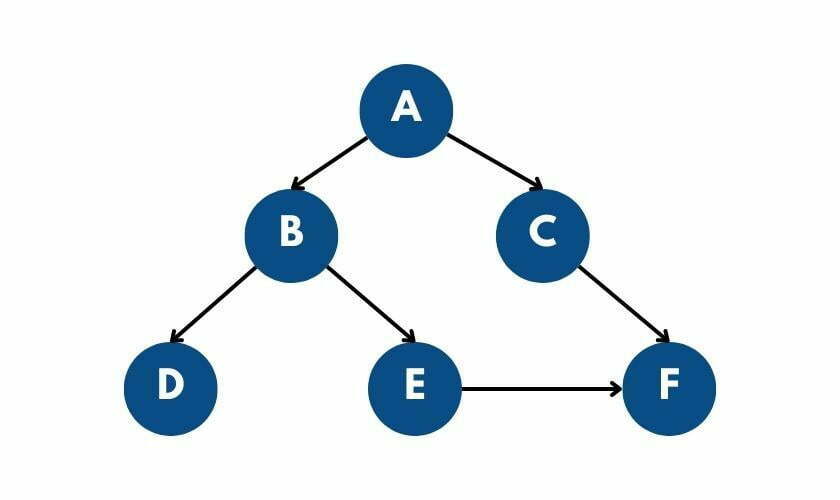
Consider the graph as input:
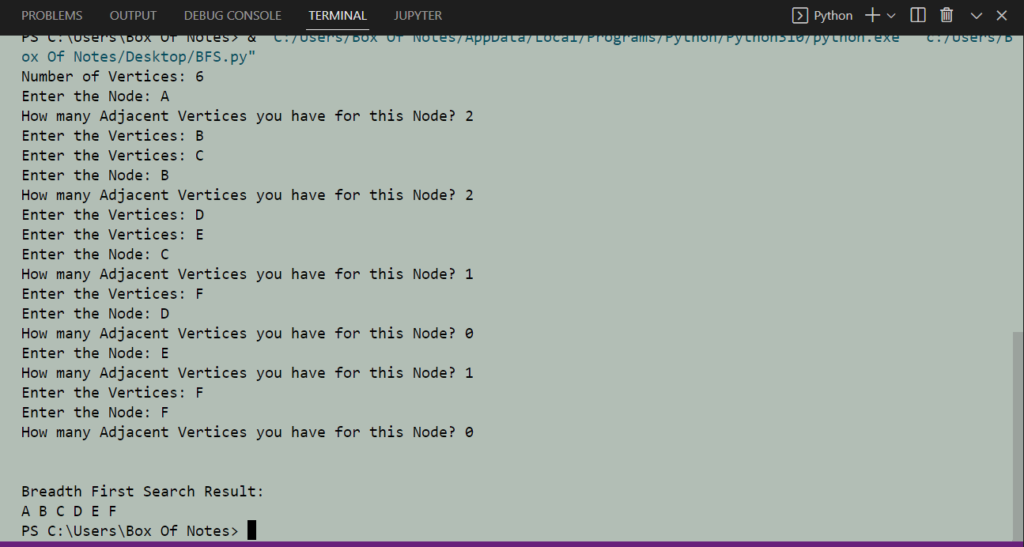
Explanation of Breadth First Search Program
Lines 1-10
We are taking input from the illustrated graph. First, take how many nodes the graph has. Then create a loop for the number, take input of the nodes and their adjacent nodes, and save them a dictionary. You can see the picture above in the Input & Output section for a better understanding.
Or you can go the easy way and replace these codes with the code below.
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : ['F'],
'D' : [],
'E' : ['F'],
'F' : []
}The illustrated graph is represented using an adjacency list. An easy way to do this in Python is to use a dictionary data structure, where each vertex has a stored list of its adjacent nodes.
Line 12
visited is a list that is used to keep track of visited nodes.
Line 13
queue is a list that is used to keep track of nodes currently in the queue.
Line 28-29
In line 28, we are setting the first key of the dictionary as the initial point or starting point.
The arguments of the bfs function are the visited list, the graph in the form of a dictionary, and the starting node res.
Lines 14-26
bfs follow the algorithm described above:
- It checks and appends the starting node to the
visitedlist and thequeue. - Then, while the queue contains elements, it keeps taking out nodes from the queue, appends the neighbors of that node to the queue if they are unvisited, and marks them as visited.
- This continues until the queue is empty.
With what you learned today and a good understanding of core python concepts, you can now easily use breadth first search in python. I hope that this article made it clear how this algorithm works.

