Water Jug Problem in Artificial Intelligence

In this article, we will learn about the water jug problem, a well-known Artificial Intelligence challenge. We will discover what this problem is, what rules were devised to address it, and what the final set of regulations was in solving the problem.

The Story of Water Jug Problem

In the water jug problem in Artificial Intelligence, we are given two jugs: one that can contain 3 liters of water and the other that can store 4 liters of water. No additional measurement equipment is accessible, and the jugs are not marked in any way. As a result, the agent’s objective here is to fill the 4-liter jug with 2 liters of water using only these two jugs and no additional materials. Both of our jugs are initially empty.

Theory for Solving the Problem

Given two jugs with capacities of max1 and max2 liters, respectively. The jugs lack marks that would allow us to measure lesser amounts. The aim is to use these two jugs to measure fill liters of water. As a result, our aim is to get from the beginning state (0, 0) to the final state (0, fill).

Solution of Water Jug Problem

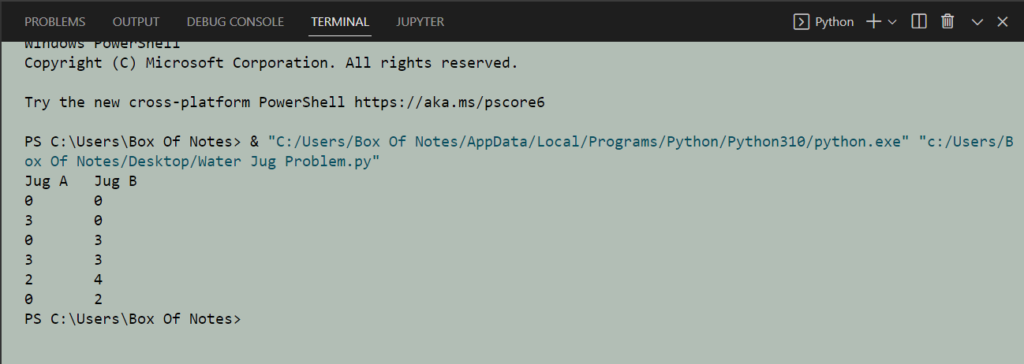
For this problem, let us assume Jug A has 3 liters and Jug B has 4 liters of water holding capacity. And we have to measure 2 litres of water and store it in Jug B. 

We will first fill Jug A with 3 litres of water and transfer this water to Jug B. So now we have Jug A with no water and Jug B with 3 Litres of water.

Then we will fill Jug A again and transfer the water to Jug B until it fills. So, now we’ll have Jug A with 2 liter of water and Jug B with 4 liter of water.

Then, we will empty the Jug B and transfer the 2 liters of water from Jug A to Jug B. And we came to the goal state.

Water Jug Problem in Python

def pour_water(juga, jugb):
    max1, max2, fill = 3, 4, 2
    print("%d \t%d" % (juga, jugb))
    if jugb==fill:
        return
    elif jugb==max2:
        pour_water(0,juga)
    elif juga!=0 and jugb==0:
        pour_water(0,juga)
    elif juga==fill:
        pour_water(juga,0)
    elif juga<max1:
        pour_water(max1, jugb)
    elif juga<(max2-jugb):
        pour_water(0,(juga+jugb))
    else:
        pour_water(juga-(max2-jugb), (max2-jugb)+jugb)
    
    
    
print("Jug A \tJug B")
pour_water(0,0)

Output