In this tutorial, you’ll learn postfix to infix conversion using stack in a C language program?
Infix Expression
The expression of the form a op b (<operand><operator><operand>). When an operator is in-between every pair of operands (A+B).
Postfix Expression
The expression of the form a b op (<operand><operand><operator>). When an operator is followed for every pair of operands (AB+).
Why do we need Infix Representation of the Expression?
Postfix notation, or reverse Polish notation, is a sentence structure for numerical expression in which the numerical administrator is constantly positioned after the operands. However postfix expressions are effectively and productively assessed by PCs, they can be challenging for people to pursue. Complex expressions utilizing standard parenthesized infix notation are in many cases more meaningful than the comparing postfix expression. Thus, we might once in a while want to permit end clients to work with infix notation and afterward convert it to postfix notation for PC handling. At times, expressions are put away or produced in postfix, and we might want to change them over entirely to infix to peruse and alter.
Examples:
Input : abc++
Output : (a + (b + c))
Input : ab*c+
Output : ((a*b)+c)
We have already discussed Infix to Postfix. Below is the algorithm for Postfix to Infix.
Algorithm
Here is the algorithm we are following for the Postfix to Infix program in C.
- Get the Postfix Expression and reverse it
- Get the String length to use for the loop
- If the scanned character is an operator, push it to stack.
- Else,
- If the scanned character is an operand, output it.
- Pop an operator from the stack.
- Reverse the string one more time.
- Print the reversed string, it is the Infix Expression for the given Postfix Expression.
Below is the implementation of the above approach:
Postfix to Infix in C Program Using Stack
Below is the code for Postfix to Infix in C program.
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
//Global Variable
char stack[50];
int top=-1;
//Function to Push Elements into Stack
void push(char ch)
{
stack[++top]=ch;
}
//Function to Pop Element From The Stack
char pop()
{
return stack[top--];
}
//function to convert from postfix to infix
void convert(char exp[])
{
int l,i,j=0;
char tmp[20];
strrev(exp);
l=strlen(exp);
for(i=0;i<50;i++){
stack[i]='\0';
}
printf("\nThe Infix Expression is : : ");
for(i=0;i<l;i++){
if(exp[i]=='+'||exp[i]=='-'||exp[i]=='*'||exp[i]=='/')
push(exp[i]);
else{
tmp[j++]=exp[i];
tmp[j++]=pop();
}
}
tmp[j]=exp[top--];
strrev(tmp);
puts(tmp);
}
//Main Function
int main()
{
char exp[50];
//taking postfix expression
printf("\nEnter the Postfix Expression : : ");
gets(exp);
//calling the function to convert the expression
convert(exp);
return 0;
}
Sample Input & Output
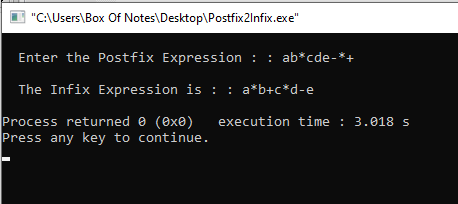
Code Explanation
Global Variable
//Global Variable char stack[50]; int top=-1;
Here, we are declaring a Stack and implementing it using an array. And declaring the top variable, because there is no element at the very beginning, that’s why the top is pointing to -1. Because the C array starts with index 0. Here, we are declaring a Stack and implementing it using an array. And declaring the top variable, because there is no element at the very beginning, that’s why the top is pointing to -1. Because the C array starts with index 0. Here, we are declaring a Stack and implementing it using an array. And declaring the top variable, because there is no element at the very beginning, that’s why the top is pointing to -1. Because the C array starts with index 0. Here, we are declaring a Stack and implementing it using an array. And declaring the top variable, because there is no element at the very beginning, that’s why the top is pointing to -1. Because the C array starts with index 0.
Push and Pop Function
//Function to Push Elements into Stack
void push(char ch)
{
stack[++top]=ch;
}
//Function to Pop Element From The Stack
char pop()
{
return stack[top--];
}Here, we are declaring the normal Push and Pop functions to perform on the stack.
Main Function
//Main Function
int main()
{
char exp[50];
//taking postfix expression
printf("\nEnter the Postfix Expression : : ");
gets(exp);
//calling the function to convert the expression
convert(exp);
return 0;
}Here, we declare an array called exp. We take the expression in exp and call the convert function.
Convert Function
//function to convert from postfix to infix
void convert(char exp[])
{
int l,i,j=0;
char tmp[20];
strrev(exp);
l=strlen(exp);
for(i=0;i<50;i++){
stack[i]='\0';
}
printf("\nThe Infix Expression is : : ");
for(i=0;i<l;i++){
if(exp[i]=='+'||exp[i]=='-'||exp[i]=='*'||exp[i]=='/')
push(exp[i]);
else{
tmp[j++]=exp[i];
tmp[j++]=pop();
}
}
tmp[j]=exp[top--];
strrev(tmp);
puts(tmp);
}We take the expression and reverse it, then get the string length. After that, we make a for loop which will fill the stack with null character. Its just a precaution measure, if you don’t want to then you can remove it from the code.
We make a for loop using string length. Then it will scan the string in order left to right. If the scanned character is an operator, then the operator will be pushed into the stack. Else, the operand will print as well pop an operator from the stack.tmp[j]=exp[top--];
It is not necessary, and the code will run without it. It’s checking if there are any operators left in the stack.
Then we again reverse the string so that it goes in the right direction.
After that all is left to Output the Result.
With what you learned today and a good understanding of core C Programming concepts, you can now easily implement Postfix to Infix in C Program.

