In this tutorial, you’ll learn how to convert infix to postfix using stack in C language program? Infix to Postfix conversion is one of the most important applications of stack.
Infix Expression
The expression of the form a op b (<operand><operator><operand>). When an operator is in-between every pair of operands (A+B).
Postfix Expression
The expression of the form a b op (<operand><operand><operator>). When an operator is followed for every pair of operands (AB+).
Why do we need a postfix representation of the expression?
The compiler scans the expression either from left to right or from right to left.
Consider the below expression: a op1 b op2 c op3 d
If op1 = +, op2 = *, op3 = +,
Then the expression will be: a + b * c + d
The compiler first scans the expression to evaluate the expression b * c, then again scans the expression to add a to it. The result is then added to d after another scan.
The repeated scanning makes it very in-efficient. It is better to convert the expression to postfix(or prefix) form before evaluation.
The corresponding expression in postfix form is abc*+d+. The postfix expressions can be evaluated easily using a stack.
Algorithm to convert Infix To Postfix
Here is the algorithm we are following for the Infix to Postfix program in C.
- Scan the infix expression from left to right.
- If the scanned character is an operand, output it.
- Else,
- If the precedence of the scanned operator is greater than the precedence of the operator in the stack(or the stack is empty or the stack contains a ‘(‘ ), push it.
- Else, Pop all the operators from the stack which are greater than or equal to in precedence than that of the scanned operator. After doing that Push the scanned operator to the stack. (If you encounter parenthesis while popping then stop there and push the scanned operator in the stack.)
- If the scanned character is an ‘(‘, push it to the stack.
- If the scanned character is an ‘)’, pop the stack and output it until a ‘(‘ is encountered, and discard both the parenthesis.
- Repeat steps 2-6 until the infix expression is scanned.
- Print the output
- Pop and output from the stack until it is not empty.
Example to better understand the Algorithm
Infix Expression: (a*b+c*(d-e)) .
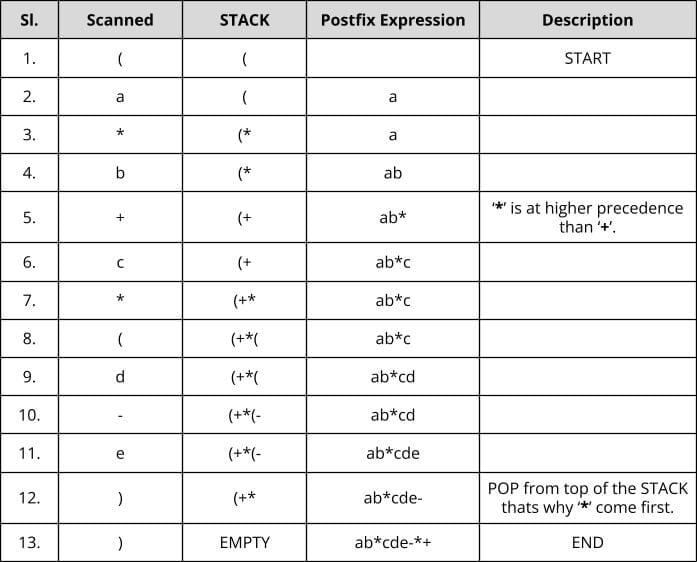
Resultant Postfix Expression: ab*cde-*+
Infix to Postfix in C Program using Stack
Below is the code for Infix to Postfix in C program.
#include<stdio.h>
char stack[20];
int top=-1;
void push(char x)
{
stack[++top]=x;
}
char pop()
{
if(top==-1)
return -1;
else
return stack[top--];
}
int priority(char x)
{
if(x=='(')
return 0;
if(x=='+' || x=='-')
return 1;
if(x=='*' || x=='/')
return 2;
}
int main()
{
char exp[20];
char *e,x;
printf("Enter the Infix Expression:: ");
scanf("%s", exp);
e=exp;
printf("\nPostfix Expression:: ");
while(*e!='\0')
{
if(isalnum(*e))
printf("%c", *e);
else if(*e=='(')
push(*e);
else if(*e==')'){
while((x=pop()) != '(')
printf("%c", x);
}
else{
while(priority(stack[top])>=priority(*e))
printf("%c", pop());
push(*e);
}
e++;
}
while(top!=-1){
printf("%c", pop());
}
printf("\n");
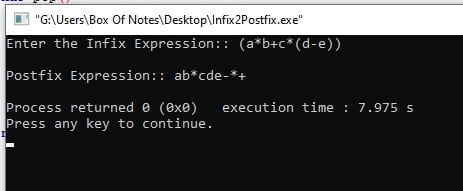
}Sample Input & Output
Code Explanation
Global variable
char stack[20]; int top=-1;
Here, we are declaring a Stack and implementing it using an array. And declaring the top variable, because there is no element at the very beginning, that’s why the top is pointing to -1. Because in C array, start with index 0.
Push and Pop Function
void push(char x)
{
stack[++top]=x;
}
char pop()
{
if(top==-1)
return -1;
else
return stack[top--];
}Here, we are declaring the normal Push and Pop functions to perform on the stack.
Priority Function
int priority(char x)
{
if(x=='(')
return 0;
if(x=='+' || x=='-')
return 1;
if(x=='*' || x=='/')
return 2;
}Priority is a very interesting function. If it sees ‘(‘, its priority is 0. If it sees ‘+’ or ‘-‘, its priority is 1, and if it sees ‘*’ or ‘/’, its priority is 2. In simple words, here, we will implement the rule of BODMAS. Or you can say we are converting Infix Expression to Postfix Expression using the order of precedence.
Main Function
char exp[20];
char *e,x;
printf("Enter the Infix Expression:: ");
scanf("%s", exp);
e=exp;We are dividing the main function into some smaller sections for better understanding. This part is basic coding. We are taking a variable called exp[20] for storing the infix expression given by the user. Then a character pointer and normal variable. And for taking input of the expression into the string called, exp[20] we are using printf() and scanf(). e = exp means, pointer e is assigned to point at the beginning of the character array exp.
while(*e!='\0')
{
if(isalnum(*e))
printf("%c", *e);
else if(*e=='(')
push(*e);
else if(*e==')'){
while((x=pop()) != '(')
printf("%c", x);
}
else{
while(priority(stack[top])>=priority(*e))
printf("%c", pop());
push(*e);
}
e++;
}This while loop will work until it reaches the null or end value of the string and *e holds the very first character of the array of exp.
The isalnum() function checks whether the argument passed is an alphanumeric character (alphabet or number) or not. in the loop, our first job is to see if it is an alphanumeric character. If it is, then it will print that character.
else if(*e=='('): If it is not an alphanumeric character then it will check for the open braces (‘(‘). If it is open braces, then it will be pushed to the stack.
else if(*e==')'): As soon as we have a closing brace (‘)‘) we have to run a loop that will pop the operator from the stack until it gets an open brace.
else{
while(priority(stack[top])>=priority(*e))
printf("%c", pop());
push(*e);
}If it is not alphanumeric or open and close braces, then it is the arithmetic operator. For this, we will use the rule of BODMAS. Bodmas stands for B-Brackets, O-Orders (powers/indices or roots), D-Division, M–Multiplication, A-Addition, S–Subtraction. We have assigned them a priority number above.
Here, we are checking the priority number of the operator, the same priority operator can sit beside each other, or a high priority operator can sit after a low priority operator, but after a high priority operator, no less priority operator can seat.
If a high priority number operator is at the top of the stack and then comes a low priority operator, then the high-priority operator will be printed. Otherwise, the new operator will push to the stack.
e++: e will increase by one (means the loop will work for the next character).
while(top!=-1){
printf("%c", pop());
}It is checking if something is still left in the stack because if that top is not equal to -1. If there are some characters, it will print the rest.
With what you learned today and a good understanding of core C Programming concepts, you can now easily implement Infix to Postfix in C Program.

