In this article, we will look at some of the most essential relationships between pixels in a digital image. As previously stated, an image is denoted by f. (x, y). This tutorial uses lowercase letters like p and q to refer to specific pixels.
Neighbors of a Pixel
A pixel p at coordinates (x, y) has four horizontal and vertical neighbors whose coordinates are given by
(x+1, y), (x-1, y), (x, y+1), (x, y-1)
This set of pixels, called the 4-neighbors of p, is denoted by N4(p).
The four diagonal neighbors of p have coordinates
(x+1, y+1), (x+1, y-1), (x-1, y+1), (x-1, y-1)
and are denoted by ND(p).
Diagonal neighbors together with the 4-neighbors are called the 8-neighbors of p, denoted by N8(p).
N8(p) = N4(p) + ND(p)
The set of image locations of the neighbors of a point p is called the neighborhood of p. The neighborhood is said to be closed if it contains p. Otherwise, the neighborhood is said to be open.

Adjacency between pixels
Let V be the set of intensity values used to define adjacency. In a binary image, V ={1} if we are referring to the adjacency of pixels with the value 1. In a gray-scale image, the idea is the same but set V typically contains more elements.
For example, in the adjacency of pixels with intensity values ranging from 0 to 255, set V might be any subset of these 256 values.
There are three types of adjacency:
- 4-adjacency: Two pixels p and q with values from V are 4-adjacent if q is in the set N4(p).
- 8-adjacency: Two pixels p and q with values from V are 8-adjacent if q is in the set N8(p).
- m-adjacency (Mixed Adjaceny): Two pixels p and q with values from V are m-adjacent if
- q is in N4(p), or
- q is in ND(p) and the set N4(p)∩N4(q) has no pixels whose values are from V.
Mixed adjacency is a modification of 8-adjacency, and is introduced to eliminate the ambiguities that may result from using 8-adjacency.
Connectivity between pixels
It is a vital topic in digital image processing.
It is used to define the boundaries of objects and region components in an image.
Let S represent a subset of pixels in an image. Two pixels p and q are said to be connected in S if there exists a path between them consisting entirely of pixels in S.
For any pixel p is S, the set of pixels that are connected to it in S is called a connected component of S. If it only has one component, and that component is connected, then S is called a connected set.
On the basis of adjacency, there are three forms of connectivity. They are as follows:
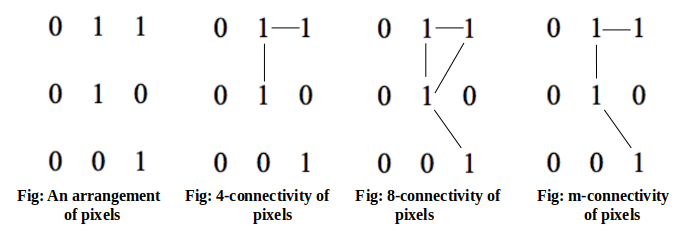
- 4-connectivity: If two or more pixels are 4-adjacent to each other, they are said to be 4-connected.
- 8-connectivity: If two or more pixels are 8-adjacent to each other, they are said to be 8-connected.
- M-connectivity: If two or more pixels are m-adjacent to each other, they are said to be m-connected.
Region
Let R represent a subset of pixels in an image. We call R a region f the image if R is a connected set.
Two regions, Ri and Rj, are said to be adjacent if their union forms a connected set.
Regions that are not adjacent are said to be disjoint. We consider 4 and 8-adjacency when referring to regions.
Boundary
The boundary is also known as the border or contour. The boundary of a region R is the set of pixels in R that are adjacent to pixels in the complement of R.
FAQ
What is adjacency in Image Processing
Two pixels are connected if they are neighbors and their gray levels satisfy some specified criterion of similarity.
